Coder un moteur graphique 3D, pour terminal Linux
Introduction
Description générale
Terminal 20 est un jeu vidéo réalisé dans le cadre du module “Initiation Projet Informatique” en semestre 2 à l’ENIB (École nationale d’ingénieurs de Brest).
Contexte et contraintes
Le jeu s’exécute directement dans un terminal UNIX, avec pour seul langage de programmation Python. Le but final est de créer un jeu qui simule un environnement de labyrinthe en 3 dimensions dans un terminal 2D en utilisant pour cela un algorithme de Raycasting. Le joueur va rencontrer des personnages non jouables qui vont lui proposer différentes énigmes et mini-jeux, s’il réussit cela lui ouvre un passage plus rapide pour la suite du labyrinthe, sinon le chemin sera plus long. Le joueur dispose d’exactement 20 minutes pour arriver à la fin du labyrinthe.
Expériences de jeu
Si le jeu se limitait exclusivement à une balade dans le labyrinthe agrémentée de quelques devinettes, il deviendrait rapidement peu attractif. C’est pourquoi dans un soucis d’amélioration de l’expérience utilisateur, deux mini-jeux sont implémentés directement dans le monde principal. Le premier consiste à un jeu de memory (à dominante fantaisie). Ce mode est proposé par le personnage nommé Nix. Voici ci-dessous une capture d’écran du gameplay proposé au joueur.
De même un second mode de jeu est proposé : il consiste en un shooter de zombie. Chaque zombie à 100 points de vie, il suffit simplement de leur tirer dessus avec un fusil lorsque que l’on les croisent sur notre chemin, à partir du moment où l’on a discuté avec le personnage nommé Rocky. Voici ci-dessous une capture d’écran du gameplay proposé au joueur.

Un point assez intéressant à aborder est la manière dont j’ai traité la gestion des tirs touchant un ennemi, au premier abord on pourrait pensé à un système complexe de rayons, mais en réalité j’ai vite abandonné l’idée d’une telle méthode¹ pour me rabattre sur une technique beaucoup plus aisée : la cible rouge au centre de l’écran étant tout le temps de la même taille peu importe l’écran utilisé, il suffit de regarder les deux petits pixels au centre de la cible (en prenant le même point de référence), si ces derniers contiennent des pixels appartenant au murs/sols, alors le joueur ne vise pas l’ennemi et aucuns PV n’est retiré à ce dernier, sinon on retire des PV à l’ennemi le plus proche du joueur (on évite de mettre plusieurs zombies à côté sur la map, pour éviter des potentiels conflits).
¹ On peut notamment penser à la situation dans laquelle un ennemi est en partie caché par l’arrête d’un mur, ce qui demanderait une nouvelle fois de projeter des rayons et de faire un choix compliqué en raison des valeurs flottantes.
Technologies utilisées
Dans cette partie je vais détailler les différents algorithmes, modules et systèmes utilisés pour rendre possible l’exécution du jeu dans son ensemble.
Modules externes
Le jeu ne pourrait fonctionner sans l’apport de différents modules développés et maintenus par la communauté. Voici une liste non exhaustive des modules importés et utilisés :
- Math : bibliothèque utilisée pour effectuer des calculs mathématique non élémentaires, primordiaux dna sle système de Raycasting, mais aussi de calcul de distance sur la carte jouable par exemple.
- Time : bibliothèque standard de Python utilisée pour gérer les opérations liées au temps. Dans ce projet, elle est utilisée pour mesurer la durée de la partie, gérer les délais dans les animations ou les interactions, et synchroniser certaines actions du jeu en fonction du temps écoulé.
- OS : La bibliothèque os en Python permet d’interagir avec le système d’exploitation, par exemple pour manipuler des fichiers, des dossiers ou obtenir des informations sur l’environnement. Dans ce projet, elle est utilisée pour récupérer la taille du terminal de l’utilisateur, ce qui permet d’adapter l’affichage du jeu à la fenêtre de chaque joueur.
- Termios : bibliothèque standard de Python utilisée pour configurer et contrôler les terminaux. Elle permet de modifier les paramètres d’entrée/sortie du terminal, comme la désactivation de l’écho des caractères saisis ou la gestion des modes non bloquants. Dans ce projet, elle est utilisée pour capturer les entrées clavier en temps réel sans nécessiter la validation par la touche “Entrée”.
- TTY : bibliothèque standard de Python utilisée pour interagir avec les terminaux. Elle est souvent utilisée conjointement avec
termiospour configurer les modes d’entrée/sortie du terminal. Dans ce projet, elle permet de capturer les entrées utilisateur en temps réel et de gérer les interactions clavier sans nécessiter la validation par la touche “Entrée”. SYS : bibliothèque standard de Python utilisée pour interagir avec l’interpréteur. Elle permet d’accéder à des fonctionnalités spécifiques du système, comme la gestion des arguments de ligne de commande, la manipulation des flux d’entrée/sortie standard, ou encore la gestion des exceptions. Dans ce projet, elle est utilisée pour capturer les arguments passés au script et pour gérer les sorties du programme.
Les deux modules suivants sont utilisés exclusivement lors de la phase de conception du jeu, et ne seront pas nécessaires pour exécuter ce dernier :
- PIL : Pillow est une bibliothèque Python utilisée pour manipuler des images. Ces fonctionnalités permettent de préparer l’image pour la conversion en art ASCII et pour l’extraction des couleurs dominantes.
- SKlearn : Scikit-learn est une bibliothèque de machine learning. Ici elle est utilisée pour identifier les couleurs principales de l’image et de les associer aux caractères ASCII pour créer des couches colorées.
Systèmes personnalisés
Comme vous avez pu le lire dans la section précédente, plusieurs systèmes ont été spécifiquement développés pour ce jeu vidéo.
Gestion de la profondeur
Si vous avez l’occasion de réaliser une partie vous constaterez que la physique inhérente à la profondeur est plutôt bien gérée par le système, en voici un exemple (sans doute anodin au premier abord mais qui relève en réalité d’une grande quantité de calcul).

- Lorsque j’ai proposé à certaines personnes de mon entourage de jouer à mon jeu (dans l’une de ses premières versions), j’ai été assez déçu du fait que la majorité des personnes avait besoin de certains temps (et d’explications) pour comprendre visuellement la disposition 3D des différents murs. Bien souvent la raison était toute trouvée : la profondeur. En effet il était difficile de comprendre quel mur était plus ou moins éloigné du joueur, la taille ne suffisant bien souvent pas. Heureusement, en réfléchissant j’en suis venu à la solution suivante :
- Définir une certaine distance autour du joueur où la couleur des murs/personnages reste inchangée.
- Cependant passé cette distance la teinte s’obscurcie de manière linéaire jusqu’à une limite maximale fixée, avec un facteur variable définit par la ligne de code suivante :
depth_factor = (1 - (max(2, min(6, cell[2])) / 8)) * 1.1cell[2]: correspond à la profondeur du pixel courant.min(6, cell[2]): limite la profondeur maximale à 6.max(2, ...): limite la profondeur minimale à 2.max(2, min(6, cell[2])) / 8: normalise la profondeur entre 2/8 et 6/8.1 - ...: inverse la valeur pour que plus la profondeur est grande, plus le facteur est petit.1.1: amplifie légèrement l’effet pour rendre la variation de couleur plus visible.
- Mais la question est : Comment savoir à quelle distance se trouve la surface du joueur ?. Enfaîte, c’est très simple, si vous n’avez pas encore consulté l’explication que j’ai réalisé concernant mon système de raycasting, je vous laisse consulter la section suivante, mais pour être assez concis, lorsque chacun de mes rayons (nombre exact de colonnes de caractères disponibles dans le terminal de l’utilisateur) entre en collision avec un mur, alors il affiche un pans de mur dont la taille est fonction de la distance entre le joueur et ce point de contact. Plutôt que d’utiliser temporairement cette donnée (comme c’était le cas auparavant), il suffit alors de stocker cette distance mesurée dans chaque liste de pixel du buffer, et ce en plus du caractère et de la couleur. Et voilà chaque caractère composant les murs à une profondeur connue.
- Les personnages : Mais là il vous vient sans doute une question à l’esprit ! Comment faire pour les personnages ? Et bien c’est encore plus simple, en effet chacun de nos PNJ ont une position exacte définie dans leur fichier texte associé, et bien il suffit d’utiliser la formule de calcul de distance entre deux points, pour attribuer une profondeur aux pixels composants le personnage : $$dist(player,npc)=\sqrt{(x_{player}-x_{npc})^{2}+(y_{player}-y_{npc})^{2}}$$
- Et enfin les éléments graphiques sont arbitrairement positionnés à une profondeur nulle pour être certains que tous les éléments de l’environnement 3D se trouvent derrière.
Et voilà nous avons maintenant un système complet pour gérer la profondeur des pixels affichés à l’écran. Dès que l’on veut modifier un pixel en particulier, par exemple si l’on veut rajouter un personnage, alors le système s’assure que le pixel à modifier dispose bien d’une profondeur inférieure à celle du pixel déjà présent à cette position, dans le buffer. Si le pixel déjà présent est plus proche de l’écran du joueur alors il n’est pas modifié.
Si vous parcourez mon code, vous constaterez qu’à l’heure actuelle le sol est définit avec une profondeur de 30, en réalité cette valeur est totalement arbitraire, il faut juste être certain que même pour des murs très éloignés, ils s’affichent bien devant le sol, car il est impossible de savoir aussi simplement qu’avec les murs à quelle distance de l’écran ils se situent.
Convertisseur ASCII
Lors de le mise en oeuvre des designs graphiques il peut devenir vite fastidieux de retranscrire un visuel pourtant simple en ASCII, certes il existe une myriade de sites web proposant de convertir des images en textes ASCII mais cela se prête bien souvent exclusivement à des images très saturées avec un fort degré d’accentuation des contours, sans cela le rendu en mono-couleur reste bien souvent approximatif. C’est pourquoi j’ai entrepris la mise en action d’un algorithme capable de transposer un fichier image en ASCII tout en conservant les nuances colorées. Pour cela des couches de couleurs sont crées, le nombre de couches désirées est laissé au choix de l’utilisateur.
On obtient par exemple les résultats suivants :
| Image initiale | Texte en sortie du convertisseur |
|---|---|
|
|
|
|
Moteur graphique
Raycasting
Le raycasting est une notion ardue, il existe par ailleurs plusieurs versions plus ou moins complexes, celle que j’utilise est sans doute l’une des plus simplistes
Le but de cette section n’est absolument pas de fournir un cours complet sur le raycasting, il y a de très bonnes ressources intéressantes disponibles sur Internet, et dont je me suis basé, voici une liste non exhaustive :
- Raycasting - Lode’s Computer Graphics Tutorial
- Terminal Dungeon - Salt Die
- Make Your Own Raycaster Part 1 - 3DSage
- Ray casting fully explained. Pseudo 3D game - WeirdDevers
- + pleins de vidéos intéressantes…
Dans les paragraphes qui suivent je parlerais avec mes propres mots pour expliquer ce que j’ai compris, avec des schémas et des exemples concrets, il se peut que je commette des erreurs dans mes explications, je vous prie de m’en excuser.
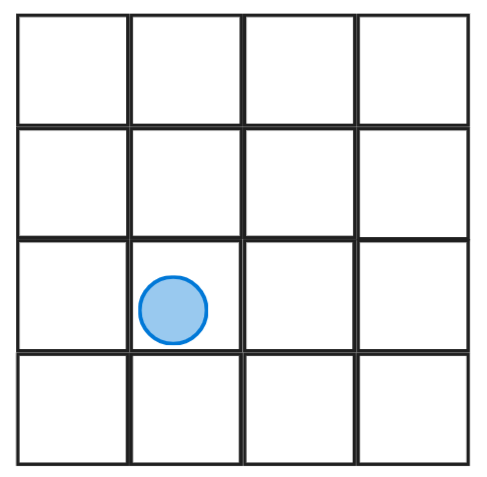
Voici une carte simplifiée de 4 par 4, le point bleu représente la position du joueur (elle peut prendre n’importe quelle valeur réelle).
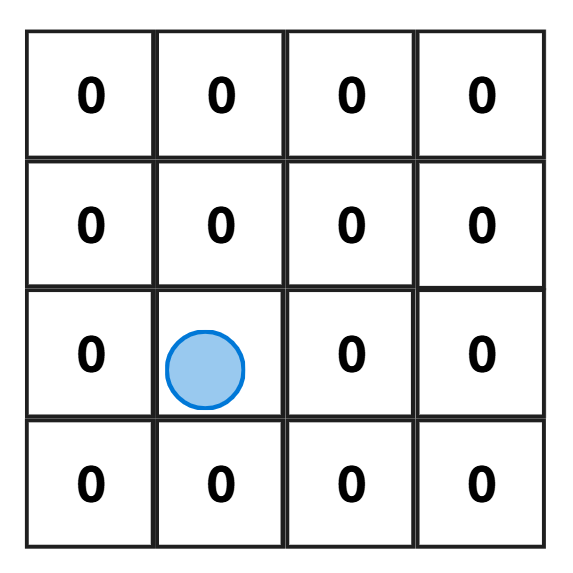
Concrètement, la carte est une liste de liste où chaque élément représente un carrée de longueur 1. Dans le cas présent le joueur se situe par conséquent à la position (x=1.4 et y=1.4). Concernant la carte, on stocke donc une matrice de 0 et de 1, où 1 représente un mur et 0 un espace vide.
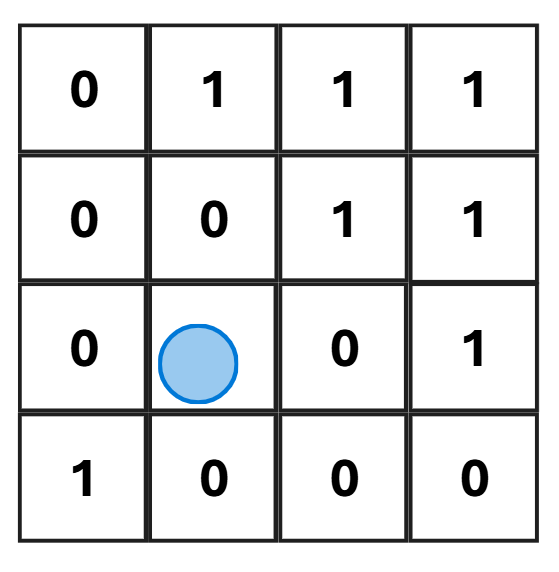
La carte est un peu vide, on choisit alors de rajouter quelques murs pour la suite de l’explication. Que l’on représentera comme suit pour la suite :
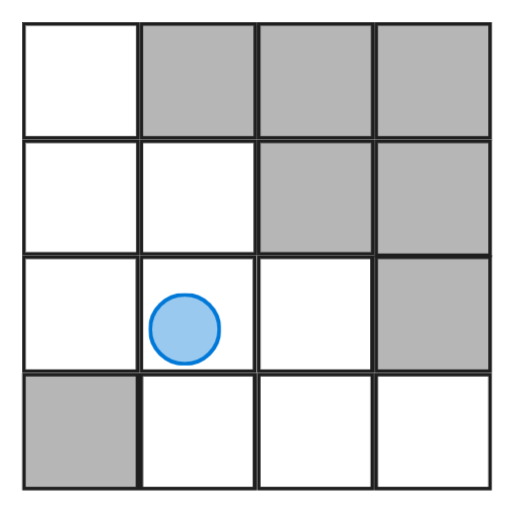
On peut maintenant passer au coeur de la technique. On projette un rayon avec un angle nul (dans le sens trigonométrique) :
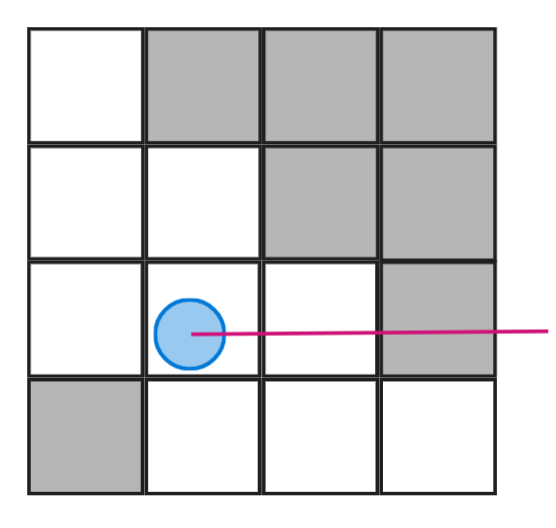
En programmation, on réalise cela en prenant la position d’un point auquel on incrémente itération après itération la composante vertical (resp. horizontale) avec une certaine quantité :
# Le rayon émis est caractérisé par un vecteur :
dx = math.cos(angle) # La composante horizontale, qui correspond au cosinus de l'angle passé en paramètre
dy = math.sin(angle) # La composante verticale, qui correspond au sinus de l'angle passé en paramètreDans le cas de notre rayon par exemple, l’angle est nul, donc dx = 1 et dy = 0.
Maintenant nous allons voir étape par étape comment détecter une collision avec un mur. Le point de départ sera la case dans laquelle se situe le joueur (et plus particulièrement le coin inférieur gauche) :
x_cellule, y_cellule = int(x0), int(y0)Sur notre représentation, on l’a marque en rose :

Il est à présent nécessaire de distinguer 4 cas, qui dépendent de la positivité de dx et dy:
dx |
dy |
Zone parcourue lors de la boucle de recherche |
|---|---|---|
| positif | positif |
|
| positif | négatif |
|
| négatif | positif |
|
| négatif | négatif |
|
D’un point de vue programmation, cela se code comme ceci :
# On fixe le pas de déplacement à incrémenter durant la recherche de collision.
# Si le cosinus de l'angle est positif, cela signifie que l'on va vers la droite.
# Sinon on va vers la gauche.
if dx > 0 :
stepX = 1
else :
stepX = -1
# Si le sinus de l'angle est positif, cela signifie que l'on va vers le haut.
# Sinon on va vers le bas.
if dy > 0 :
stepY = 1
else :
stepY = -1Cela va devenir un tout petit plus complexe à partir d’ici. Ce qui nous intéresse maintenant c’est de connaître le premier axe vertical et horizontal que notre rayon va rencontrer. Dans notre cas dy est nul, ce qui signifie que notre rayon ne croisera jamais d’axe horizontal, l’algorithme ne cherchera donc pas une collision horizontale.
On se focalise donc sur la composante x, car cette dernière rentrera bien en collision avec un axe vertical (représenté en vert). Ici il s’agira du bord droit de la case étudiée mais je vais vous mettre deux autre exemples de rayons avec des angles différents pour bien comprendre.
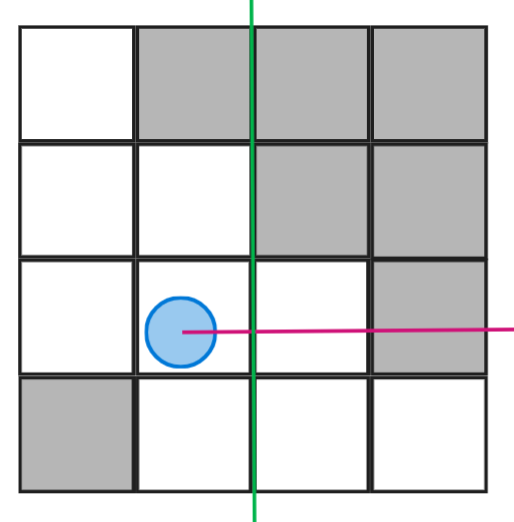
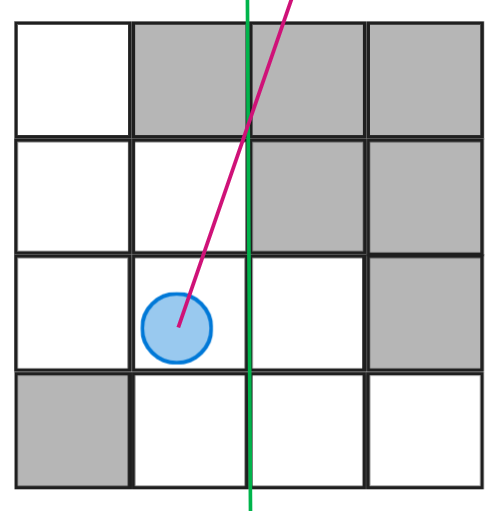
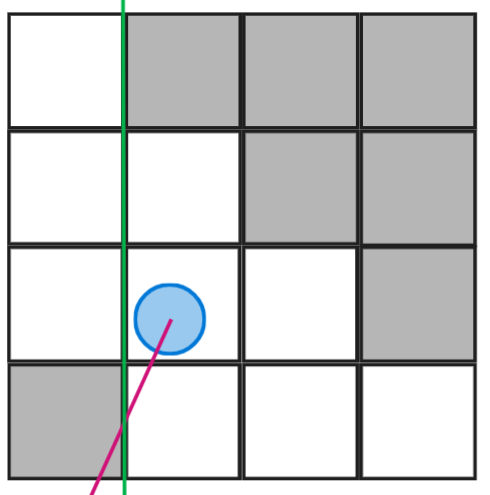
Je pense que vous avez saisi le fait qu’il suffit de regarder le signe de dx pour connaître l’axe vertical franchi (droite ou gauche) à partir de la cellule où se situe le joueur. Il suffit de suivre exactement le même raisonnement pour les axes horizontaux en fonction de dy.
Bon je ne vous ai pas tout dit… Enfaîte ce qui nous intéresse réellement c’est de savoir si l’on franchit d’abord un axe vertical ou horizontal. Pour cela nous allons avoir besoin d’un peu de trigonométrie. On se concentre une nouvelle fois sur dx, on zoome sur la case où se situe le joueur, je rappelle qu’il a une abscise de 1.4 ! Ici pour rendre le schéma un peu plus parlant (et éviter que les droites se superposent) nous allons temporairement considérer que le rayon a un angle de pi/4 et non 0. La valeur recherchée c’est l’hypoténuse, et justement cela tombe bien car nous avons assez d’informations pour le déterminer. En effet, il s’agit simplement de : hypoténuse = adjacent/cos(angle).
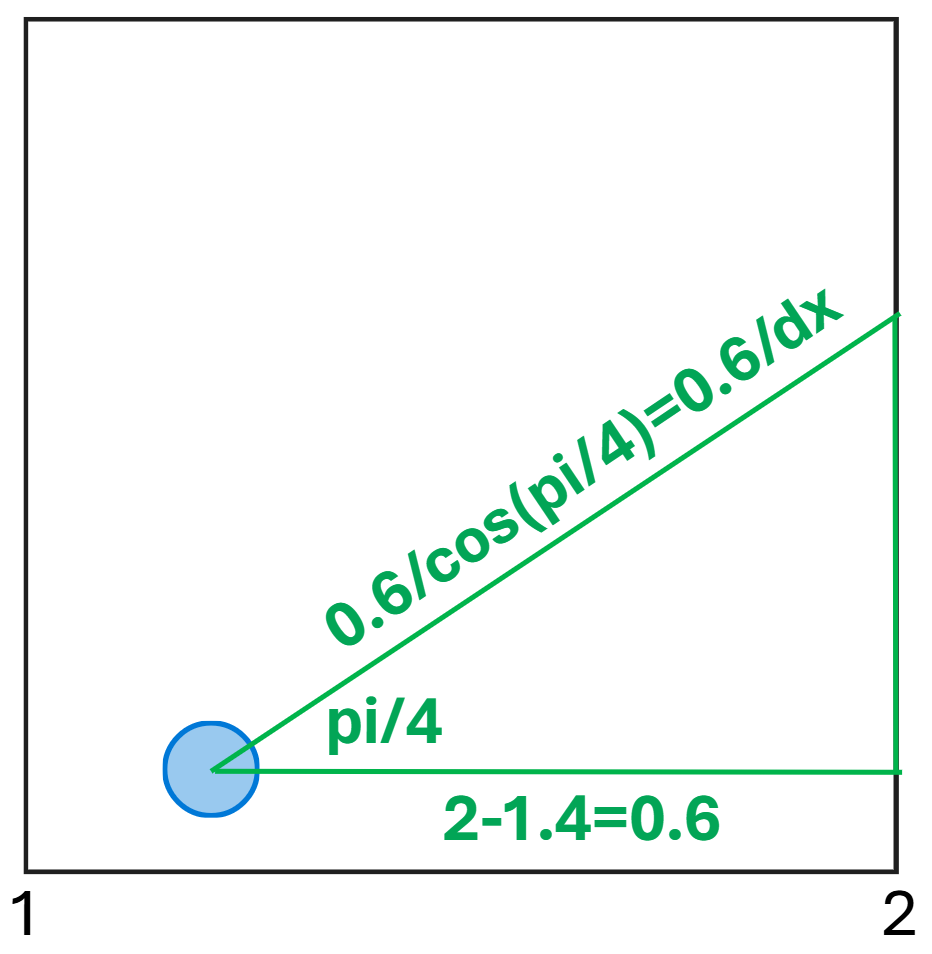
Et voilà on connaît maintenant la distance exacte entre le joueur est la première surface verticale possible. Dans le cas où dx est nul, on considère cette distance comme infinie.
Pour les besoins de notre boucle de recherche de collisions, on enregistre aussi la distance à parcourir entre deux bordures verticales de la grille avec un axe dx. Cela permet de toujours se déplacer d’un carré vers la droite dans ce cas précis, en ayant pour référentiel dx, et non l’axe des abscises traditionnel. Concrètement c’est l’hypoténuse du triangle suivant :
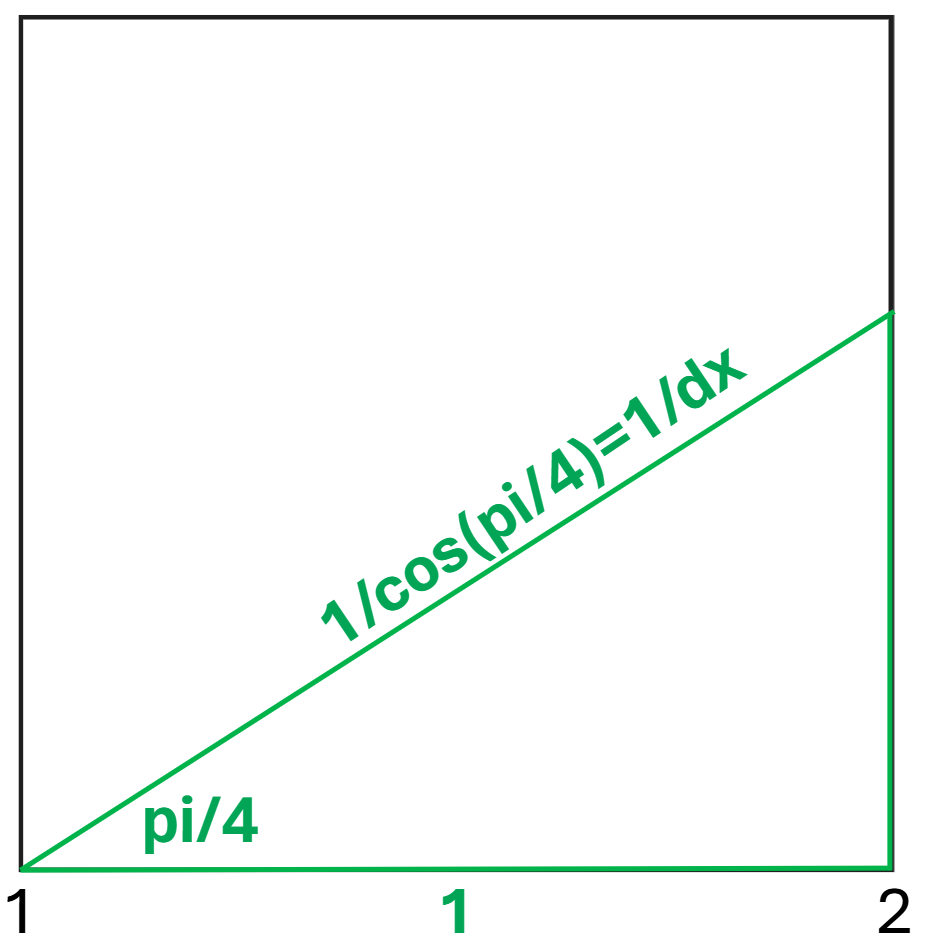
Je le redis une nouvelle fois ici, mais il faut refaire exactement la même chose pour dy. Cela correspond au calcul suivant pour les collisions avec les axes horizontaux :
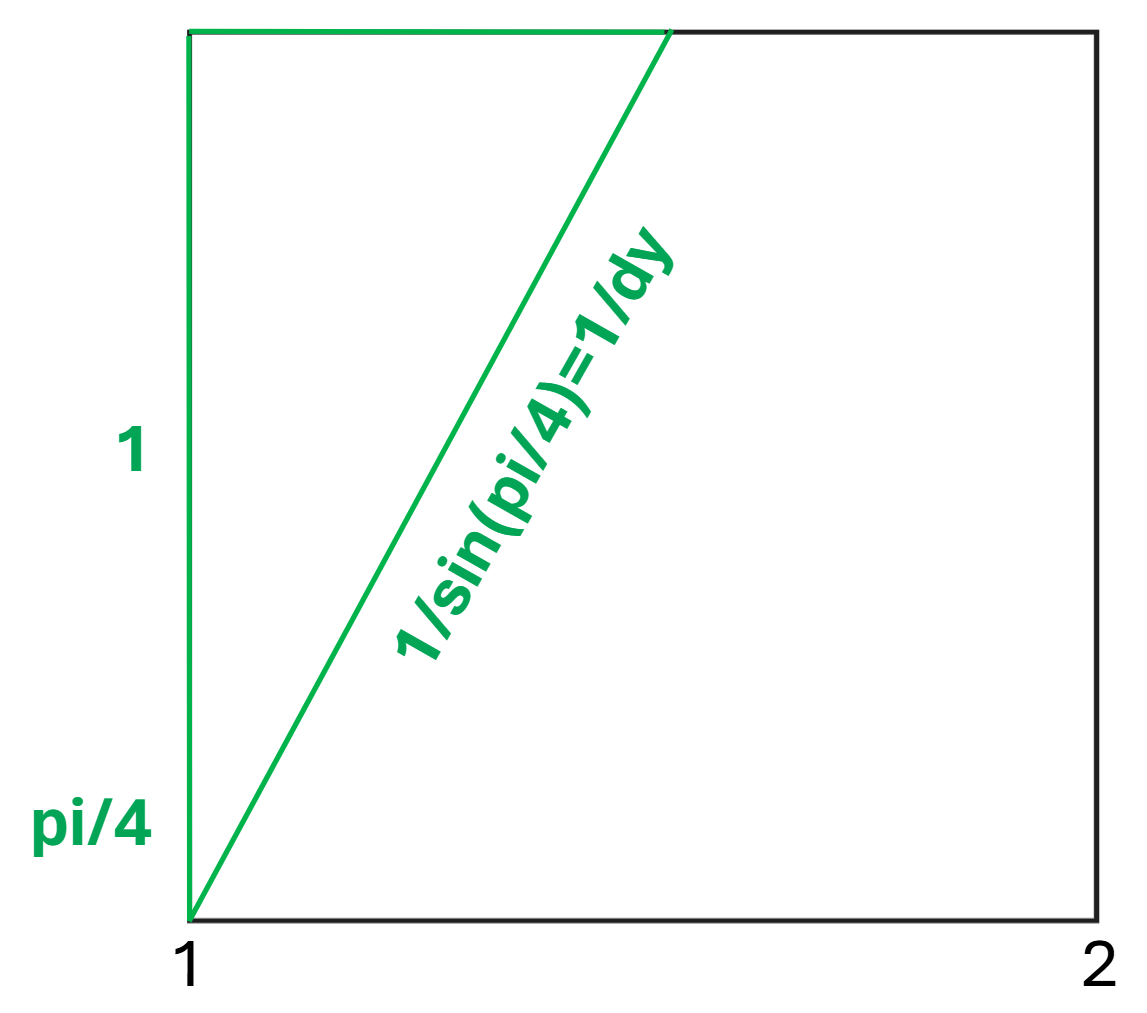
D’un point de vue purement algorithmique, le code est le suivant :
if dx != 0:
if dx > 0 :
next_x = x_cellule + 1 # Abscisse du prochain bord vertical de cellule que le rayon atteindra.
else :
next_x = x_cellule # Vu que le rayon va vers la gauche, le prochain axe vertical qu'il va rencontrer est celui à l'origine de la cellule où il se trouve.
# tmaxX et tmaxY vont nous permettent de savoir si le rayon atteint en premier le bord de cellule horizontal ou vertical.
# Ici la première valeur attribuée à tmaxX correspond à la distance entre le point exact du joueur dans la cellule et la première bordure verticale, en empruntant l'axe dx.
# Ce calcul résulte directement d'une formule trigonométrique de base : hypoténuse = adjacent/cos(angle)
# Ici l'hypoténuse c'est la longueur du segment pris sur le rayon entre l'abscisse du joueur et l'abscisse du prochain axe vertical de la grille,
# le côté adjacent (next_x - x0) c'est la longueur prise entre l'abscisse du joueur et le même axe vertical, mais avec un angle nul cette fois-ci.
tmaxX = (next_x - x0) / dx
tDeltaX = abs(1 / dx) # tDeltaX représente la distance à parcourir entre deux bordures verticales de la grille avec un axe dx
# Ici l'hypoténuse c'est la longueur du segment pris entre deux bordures verticales (tDeltaX), et le côté adjacent c'est la longueur d'une cellule : 1
else:
tmaxX = float('inf') # Si le cosinus est nul, cela signifie qu'il est impossible d'atteindre la prochaine bordure verticale, que ce soit vers la droite ou vers la gauche.
# Le raisonnement est le même que pour les abscisses mais avec les ordonnées :
if dy != 0:
if dy > 0 :
next_y = y_cellule + 1
else :
next_y = y_cellule
tmaxY = (next_y - y0) / dy
tDeltaY = abs(1 / dy)
else:
tmaxY = float('inf')Il ne reste plus qu’à parcourir l’ensemble des cases traversées par le rayon. Comparer l’hypoténuse du triangle rectangle associé aux axes horizontaux avec celui associé aux axes verticaux permet de savoir aisément quelle case est la prochaine à être parcourue.
On fixe une longueur notée max_distance qui est la limite à partir de laquelle la boucle s’arrête si elle n’a pas trouvé de collision avec un mur (La fonction retournera alors None). Mais intéressons nous plus en détail avec le cas où il y a bien une collision avec un mur. Nous avons vu plus haut comment parcourir le trajet du rayon case après case, et bien pour savoir si il y a une collision avec un mur il suffit tout simplement de regarder si la prochaine case à parcourir contient un 1. Si c’est le cas, on calcule le point d’impact du rayon, en ayant le référentiel de la carte:
$$ impact_{x} = x_{player} + distance \times dx $$ $$ impact_{y} = y_{player} + distance \times dy $$
où $distance$ représente la somme de tous les hypoténuses minimaux, calculés durant l’itération.
On a donc la boucle while suivante :
distance = 0 # Compteur de la distance parcourue par le rayon depuis la position du joueur
while distance < max_distance : # Tant que le rayon est inférieur à la distance maximale désignée par l'utilisateur, il continue à explorer les cellules suivantes quie se trouvent sur son cap.
if tmaxX < tmaxY : # Cette situation a lieu lorsque le rayon touche d'abord l'axe vertical
x_cellule += stepX # On incrémente d'une cellule vers la droite ou vers la gauche (en fonction de la valeur de stepX)
distance = tmaxX # La distance correspond donc toujours à : (nombre de cellules traversées depuis la position du joueur) × (la distance nécessaire pour traverser une cellule) + distance entre le joueur et la première bordure.
tmaxX += tDeltaX
else : # Cette situation a lieu lorsque le rayon touche d'abord l'axe horizontal (le raisonnement est identique au cas précédent mais verticalement ici)
y_cellule += stepY
distance = tmaxY
tmaxY += tDeltaY
if 0 <= x_cellule < len(Game.get_map(game_inp)[0]) and 0 <= y_cellule < len(Game.get_map(game_inp)) :
if Game.get_map(game_inp)[y_cellule][x_cellule] == 1:
# On calcule les coordonnées exactes du point d'impact en fonction du déplacement du rayon :
impact_x = x0 + distance * dx
impact_y = y0 + distance * dy
return (impact_x, impact_y, distance)Et c’est ainsi que nous avons développé une fonction permettant de connaître le point d’impact d’un rayon partant d’un joueur avec un mur disposé sur la map.
Mais un rayon ne suffit évidemment pas, en réalité il faut définir un certain angle de vision, que l’on divise par le nombre de colonnes de caractères disponibles dans le terminal de l’utilisateur. Donc pour chaque colonne, on projette un rayon avec un certain angle par rapport au centre de l’écran. Graphiquement cela donne ça (bien sûr il y a autant de rayons que de colonnes sur le terminal utilisateur, donc ci-dessous le nombre de rayons est largement inférieur au nombre réel.) :
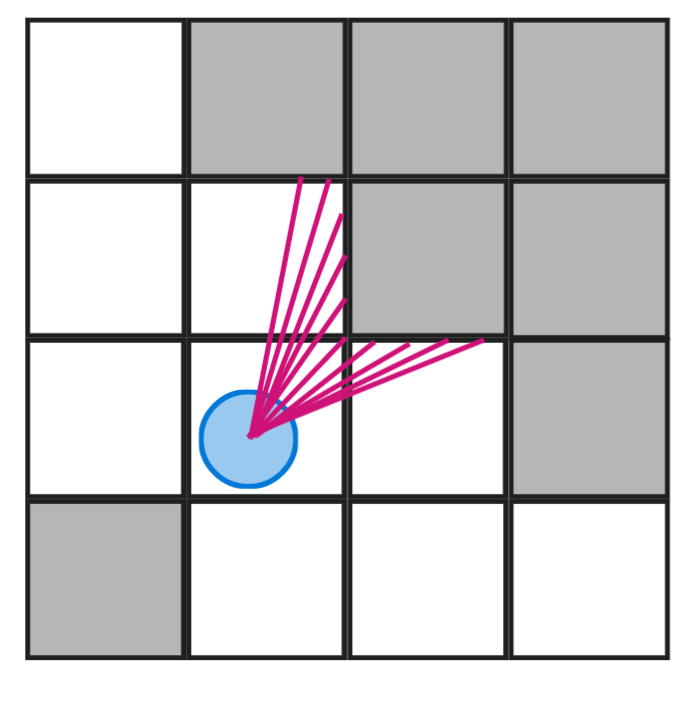
Et enfin, il ne reste plus qu’à dessiner une colonne de pixels pour chaque rayon. Concrètement, on se positionne sur la ligne au centre de l’écran et pour chaque colonne, de l’extrême gauche à l’extrême droite, on envoie un rayon, dont la fonction étudiée plus tôt nous renvoie la distance de collision avec le prochain mur. Il suffit d’afficher une colonne de pixels dont la hauteur² est : $lineHeight = \frac{hauteur_{écran}}{distance_{rayon}}$
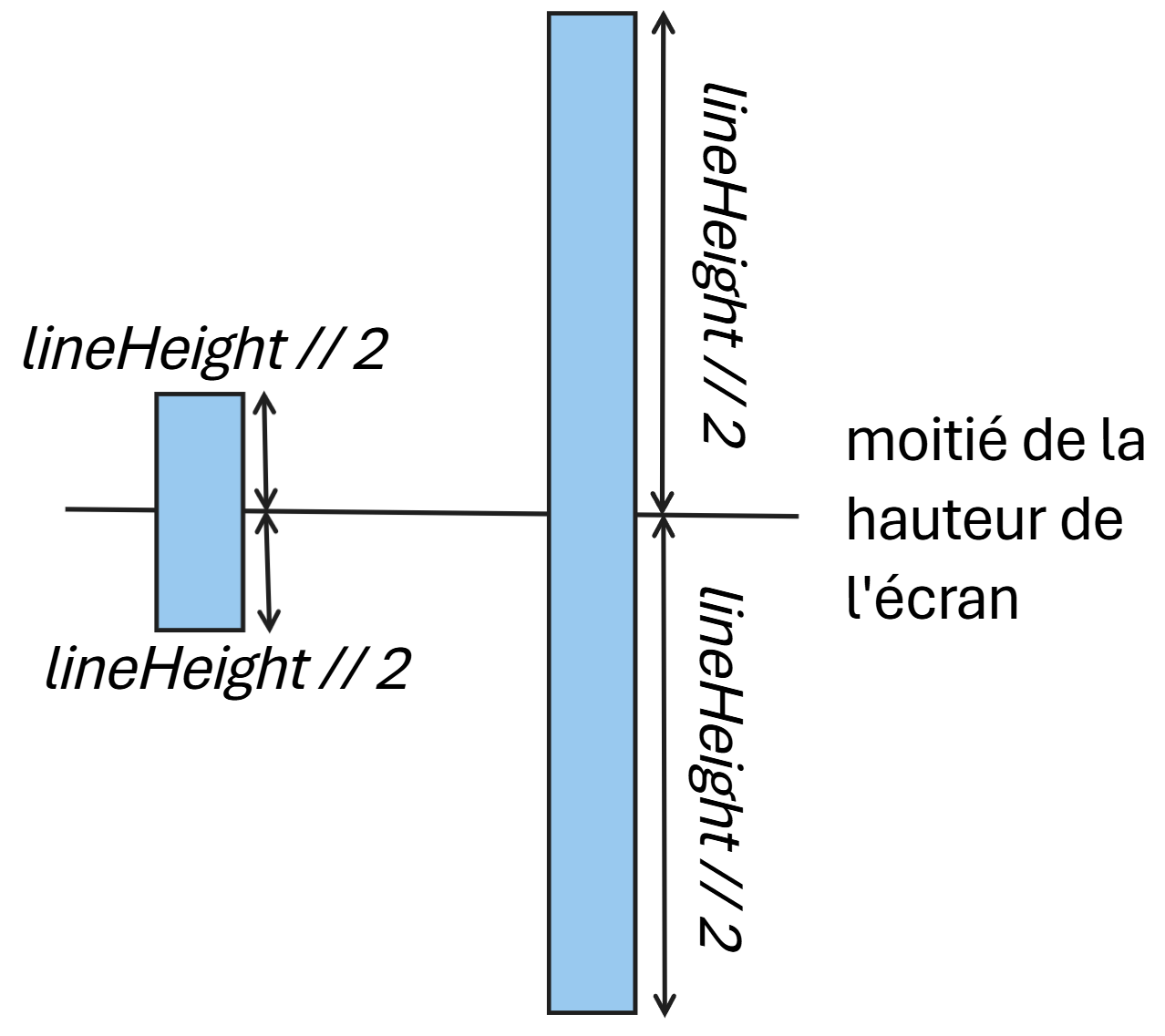
Ici c’est pareil, il y a autant de colonnes (avec des hauteurs différentes) que de colonnes disponibles dans le terminal donc il faut imaginer l’écran rempli. Si vous avez bien compris, il doit être évident que la colonne à gauche représente un mur très éloigné alors que la colonne à droite représente un mur très proche du joueur.
² Les plus matheux d’entre vous ont sûrement constaté qu’un tel système ne produit pas une image plane de l’environnement. En effet, cela donne une vision arrondie plus on s’éloigne du centre de l’écran. D’ailleurs vous le connaissez sûrement cet effet : l’effet fisheye, oui le même que sur les filtres marrants sur votre téléphone !

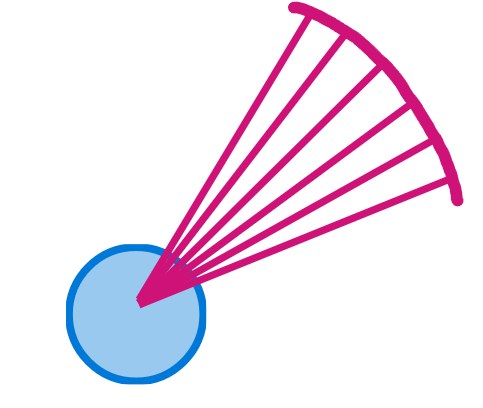
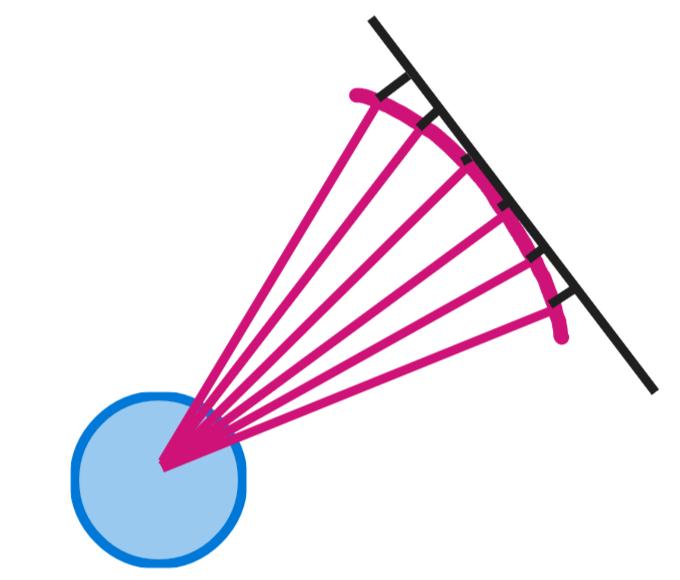
La solution est assez simple, il suffit de projeter les rayons sur une tangente pour aplanir l’image. Pour cela, on multiplie la distance du rayon par cosinus(2pi) ou cosinus(-2pi), en fonction de la positivité de l’angle entre le joueur et le rayon.
# Correction de l'effet "fish-eye" :
angle_fix = player_angle - ray_angle
if angle_fix < 0 :
angle_fix += 2*PI
elif angle_fix > 2*PI :
angle_fix -= 2*PI
ray_distance = ray_distance * math.cos(angle_fix)Reste à mettre en place un terrain d’entente pour que le formalisme du convertisseur ASCII soit pleinement interprété par le moteur graphique. Cette problématique est détaillée à cet endroit : Formalisme des données
Système de buffering
Ce module est conçu pour afficher des caractères dans le terminal tout en permettant de contrôler leur position et leur couleur.
- Un “buffer” est comme une feuille de papier quadrillée où chaque case peut contenir un caractère, une profondeur et une couleur associée. Cette feuille est utilisée pour préparer ce qui sera affiché à l’écran. Cela permet de modifier et organiser les éléments avant de les montrer, plutôt que de les afficher directement. Chaque case du buffer contient trois informations : Le caractère à afficher (par exemple, une lettre ou un symbole), la couleur du caractère, définie par des valeurs de rouge, vert et bleu (RGB) et une valeur réelle, représentant la profondeur du pixel par rapport à la position courante du joueur.
- Le module permet de créer un buffer de dimensions personnalisées (largeur et hauteur). Une fois créé, ce buffer est rempli par défaut avec des espaces blancs (caractères vides), une couleur blanche et une profondeur infinie. Lorsqu’un buffer est créé, il est “nettoyé” pour s’assurer qu’il est vide et prêt à être utilisé. On peut, par la suite, définir ou modifier la largeur et la hauteur du buffer à tout moment.
- Le module permet d’insérer des caractères dans le buffer à des positions spécifiques. Par exemple, on peut placer une lettre “A” en rouge à une certaine case de la feuille. Si on insère une chaîne de plusieurs caractères (comme “Bonjour”), chaque lettre est placée dans une case consécutive, en partant de la position spécifiée. Chaque caractère peut avoir une couleur différente, ce qui permet de créer des affichages colorés.
- Une fois le contenu du buffer prêt, il est affiché dans le terminal. Le module utilise des commandes spéciales pour déplacer le “curseur” du terminal à la bonne position avant d’afficher chaque ligne. Cela garantit que les caractères apparaissent au bon endroit. Avant d’afficher un caractère, le module vérifie si sa couleur est différente de la précédente. Si c’est le cas, il change la couleur active dans le terminal pour correspondre à celle du caractère. Une fois tous les caractères affichés, le terminal est réinitialisé pour revenir à son état normal.
- L’utilisation d’un buffer permet de contrôler précisément ce qui est affiché à l’écran, sans avoir à effacer et réécrire constamment. Cela rend l’affichage plus fluide et évite les scintillements.
Gestion des entrées
Le module Tools.py est capable de capturer les touches pressées par l’utilisateur dans un terminal, sans nécessiter la validation par la touche “Entrée”.
- Dans un terminal classique, lorsqu’on tape une touche, celle-ci n’est généralement pas immédiatement envoyée au programme. Il faut appuyer sur “Entrée” pour valider l’entrée. Ce comportement est pratique pour écrire des commandes, mais il n’est pas adapté pour des applications interactives comme des jeux. Ce module permet de contourner ce comportement en capturant directement les touches pressées, sans attendre “Entrée”. Cela permet de réagir instantanément aux actions de l’utilisateur.
- Pour modifier le comportement du terminal, le module utilise une bibliothèque appelée
termios. Cette bibliothèque permet de configurer les paramètres d’entrée et de sortie du terminal. Par défaut, le terminal affiche chaque touche pressée (mode “ECHO”) et attend “Entrée” pour valider l’entrée (mode “CANONIQUE”). On effectue donc la modification temporaire suivante sur la configuration du terminal utilisateur: désactivation de l’ECHO (Les touches pressées ne sont pas affichées à l’écran) et désactivation du mode canonique (Les touches sont immédiatement envoyées au programme, sans attendre “Entrée”). - Une fois le terminal configuré, le module attend que l’utilisateur appuie sur une touche. Dès qu’une touche est pressée, son code ASCII (un nombre représentant le caractère) est capturé et renvoyé au programme. En effet, chaque touche du clavier est associée à un code numérique unique. Par exemple : La touche “A” a le code 65. La touche “a” a le code 97. La touche “Entrée” a le code 13. Le programme peut ensuite utiliser ce code pour déterminer quelle action effectuer.
- Après avoir capturé la touche, le module restaure les paramètres d’origine du terminal. Cela garantit que le terminal revient à son comportement normal une fois l’interaction terminée.
Formalisme des données
Les données concernant les personages non jouables (NPC) sont encapsulées dans un fichier texte respectant une certain formalisme pour que le module NPC interprète correctement les différents valeurs attribuées. En voici un court extrait du personnage CHUCK pour bien entrevoir la mise au point du système de téléversement :
__NAME__CHUCK
__POSITIONX__17.5
__POSITIONY__18
__NBTEXTS__7
__COSTUME__1
Arrrhhhh, satanée bûche, je vais y passer la soirée à ce rythme là...
__COSTUME__2
Oh salut, t'es nouveau ? On s'est jamais vu ici je crois, moi c'est CHUCK !
__COSTUME__1
Comme tu peux le voir je suis un peu dans la galère, le soleil va bientôt se coucher et il me reste une tonne de bûche à couper pour chauffer mon foyer...
__COSTUME__2
Oh mais c'est rare de voir des gens habillés comme toi dans le coin. Tu dois être doué avec les chiffres.
__COSTUME__2
Tu tombes bien j'ai une question pour toi, bon tu vois je suis payé par un mec pour te donner l'accès à la suite du labyrinthe si tu m'aides.
__COSTUME__2
Mais par contre si tu te trompes, tu vas devoir marcher beaucoup plus longtemps, mais bon cela te fera les pattes, AHAHAH !
__COSTUME__1
Bon assez bavardé, je sais que ton temps est précieux, le miens aussi d'ailleurs. Voici la fameuse question :
__QUESTION__Il me faut 1min32s pour couper une bûche en deux. Combien de temps me faut-il pour couper une bûche en 16 morceaux de même taille ?
__REPONSE__13 minutes
__NBBLOCKS__2
15,19
15,27
__REPONSE__23 minutes
__NBBLOCKS__2
17,19
17,27
__REPONSE__11,5 minutes
__NBBLOCKS__2
19,19
14,29
__VISUAL0__
__NBCOLORS__7
__COLORR__226
__COLORG__150
__COLORB__90
__COLORR__59
__COLORG__39
__COLORB__24
1111111111111111111111111111111=++=111111111111111111111111111111111
1111111111111111111111111111+%%%%%%%%*111111111111111111111111111111
111111111111111111111111111#%%%%%%%%%%%=1111111111111111111111111111
1111111111111111111111111=%%%%%%%%%%%%%%*111111111111111111111111111
1111111111111111111111111=%%%#111111111%*111111111111111111111111111
1111111111111111111111111=%%%11%%%#1#%%%=111111111111111111111111111
1111111111111111111111111#1*%1111111%11#=111111111111111111111111111
1111111111111111111111111=#*%#1111##%11%=111111111111111111111111111
11111111111111111111111111=%%%%#%%%%%%%%+111111111111111111111111111
111111111111111111111111%*#%%%%%%%%%%%%%*111111111111111111111111111
111111111111111111111%%111*#%%%%%%%%%%%%%%%1111111111111111111111111
111111111111111111+#%1111111111%%%%%%%11111%+11111111111111111111111
111111111111111=%%111111111111111111111111111%%111111111111111111111
.
.
.
__ENDVISUAL__Auteur : Romain MELLAZA
Date de publication : 23 Juin 2025







